Over the course of the last few weeks, I’ve dove into the wide world of algorithms in computer programming. Although they can be intimidating at first, constructing algorithms is just the coding version of solving a puzzle, which activates the creative problem-solving capacity of your brain and can actually become quite fun.
At a high level, an algorithm is just a procedure for taking an input of data (which can consist of words, numbers, or other data types), and transforming that data into some form of desired end result.
Approaching an algorithm question for the first time is a daunting task. Your first reaction might be to start writing code, but more often than not that will not prove useful. Instead, I like to follow a process that delays the actual code writing until the problem is fully understood.
Let’s step through solving an algorithm with a practice problem.
“Given an input n, where n is less than or equal to 50, calculate that input’s value in the Fibonacci sequence."
The Fibonacci sequence is a famous mathematical construct of a group of integers where each number is the sum of the previous two. Here's an example of the sequence revealing itself in nature.
1. Read the Problem
Maybe this sounds stupid, but it’s important to read the problem meticulously and truly understand the task at hand. Ask yourself what the desired end result is and think about the different paths with which you might be able to get there. In this instance, we want to calculate a number based on the two numbers that came before it in a certain sequence.
For more challenging problems, this process can actually take some time, which is OK. It will probably end up saving you time in the long run!
2. Solve an example manually
An example for our problem here could be n = 7. Or, in English, what is the value of the 7th integer in the Fibonacci sequence?
The important part of going through this process is not just to achieve the desired end result, but also to identify any repeatable rules or tasks that we can imply. These rules will become important aspects of our code once we start writing.
- First, we’ll have to start build the Fibonacci sequence, starting with 1 and 1 as our first 2 integers.
- Second, we’ll have to add the previous two numbers to calculate the next value.
- 1 + 1 = 2 (This is our 3rd value)
- 1 + 2 = 3 (4th)
- 2 + 3 = 5 (5th)
- 3 + 5 = 8 (6th)
- 5 + 8 = 13 (7th)
- Third, we’ll want to take that final value, 13 and print it or return it to the program to use it somewhere else.
At this point, we’ll also want to consider edge cases: situations where our normal rules might need to be broken. In this relatively simple example, I can't think of any right now, but it's a good thing to keep in the back of your head as you go through the problem-solving process.
3. Pseudo-code
Based on our manual example, let’s write out some comments that describe exactly what we want our program to do.
Initiating the process with some pseudo-code can help alleviate coder's block and get the ball rolling on a tricky problem. It's also a great way to ensure you don't skip any steps while translating the manual example to a working program.
4. Code it!
Our Ruby code below simply follows the comments laid out by the pseudo code. If you’re relatively new to programming, you might be confused about how we’re able to call the method fibonacci from inside itself. This utilizes a recursive strategy, which you can learn more about here.
The simple program above outputs the following:
At this point, we've achieved our initial goal! We're able to correctly produce the desired output of our test case, and by changing the input method from n = 7 to n = rand(1..50), we can test our program for all of the problem's cases.
5. Refactor
If you’re a programmer dealing with algorithms, a helpful mantra to maintain is “Can we do it better?” Any initial code written to fix a bug or build a feature is unlikely to be the best way of approaching solving a problem.
In this example, we’ve actually written some downright troubling code. Our fibonacci method has an exponential runtime, meaning that as the input n increases, it will take more and more time to run the method. Let's add in Ruby's benchmark module to output not only the result but also how long it took to run.
As n increases, we can now evaluate our program's runtime and determine whether or not it's a workable solution we'd feel comfortable using in a production app. Unfortunately, somewhere between n = 35 and n = 45, the runtime takes a dramatic turn for the worse. Evaluating fibonacci(45) actually takes over 3 minutes!
Uh-oh......
This graphical demonstration of runtimes (also known as Big-O notation) demonstrates that as long as n is a relatively small number, we won’t really run into any problems. But once we pass a certain tipping point, the lag in our application will actually become quite drastic.
At this point, let’s return to our code and evaluate how we might be able to reduce the runtime to a more realistic timeframe. Our current problem is that each operation contains two sub-operations, unnecessarily complicating the code and making each evaluation longer than the once before it.
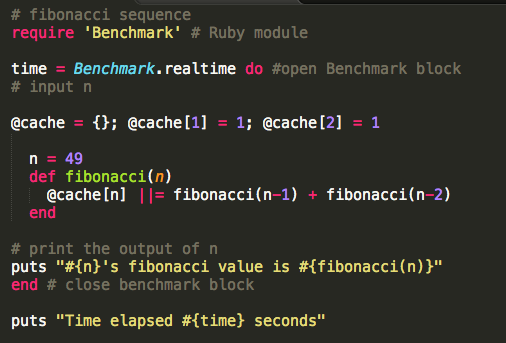
One way to approach this is to cache our data as we move through the method, meaning we'll sacrifice some disk space as we hold on to data longer, but it'll be worth it because we're able to evaluate inputs significantly faster. I'll also refactor the first part of the simple if statement into a more concise cache statement. Here's the potential solution:
The important part here is the output. We can now evaluate the higher numbers in the range almost instantaneously!
At this point, I'll leave the algorithm alone for now. Although the code isn't perfect, the performance is solid and it accurately completes the original desired output. When some potential improvement comes to me later, I'll definitely refactor it again.